Note

Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder

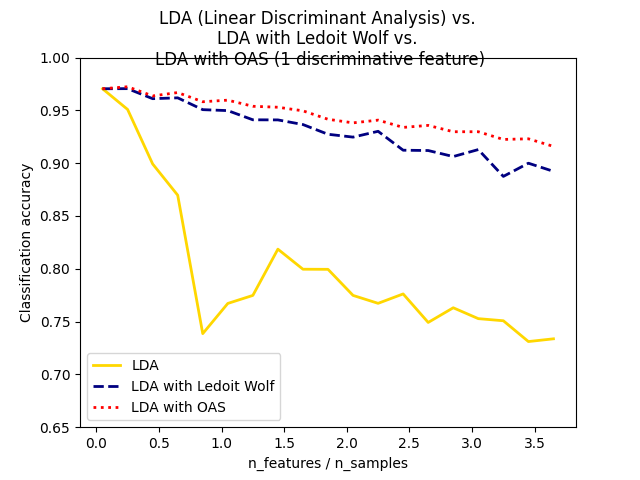
Normal, Ledoit-Wolf and OAS Linear Discriminant Analysis for classification#

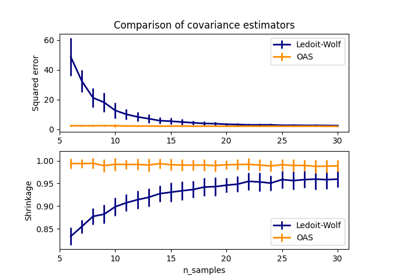
This example illustrates how the Ledoit-Wolf and Oracle Approximating Shrinkage (OAS) estimators of covariance can improve classification.

LDA (Linear Discriminant Analysis) vs. LDA with Ledoit Wolf vs. LDA with OAS (1 discriminative feature)

import matplotlib.pyplot as plt
import numpy as np

from sklearn.covariance import OAS
from sklearn.datasets import make_blobs
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

n_train = 20  # samples for training
n_test = 200  # samples for testing
n_averages = 50  # how often to repeat classification
n_features_max = 75  # maximum number of features
step = 4  # step size for the calculation


def generate_data(n_samples, n_features):
    """Generate random blob-ish data with noisy features.

    This returns an array of input data with shape `(n_samples, n_features)`
    and an array of `n_samples` target labels.

    Only one feature contains discriminative information, the other features
    contain only noise.
    """
    X, y = make_blobs(n_samples=n_samples, n_features=1, centers=[[-2], [2]])

    # add non-discriminative features
    if n_features > 1:
        X = np.hstack([X, np.random.randn(n_samples, n_features - 1)])
    return X, y


acc_clf1, acc_clf2, acc_clf3 = [], [], []
n_features_range = range(1, n_features_max + 1, step)
for n_features in n_features_range:
    score_clf1, score_clf2, score_clf3 = 0, 0, 0
    for _ in range(n_averages):
        X, y = generate_data(n_train, n_features)

        clf1 = LinearDiscriminantAnalysis(solver="lsqr", shrinkage=None).fit(X, y)
        clf2 = LinearDiscriminantAnalysis(solver="lsqr", shrinkage="auto").fit(X, y)
        oa = OAS(store_precision=False, assume_centered=False)
        clf3 = LinearDiscriminantAnalysis(solver="lsqr", covariance_estimator=oa).fit(
            X, y
        )

        X, y = generate_data(n_test, n_features)
        score_clf1 += clf1.score(X, y)
        score_clf2 += clf2.score(X, y)
        score_clf3 += clf3.score(X, y)

    acc_clf1.append(score_clf1 / n_averages)
    acc_clf2.append(score_clf2 / n_averages)
    acc_clf3.append(score_clf3 / n_averages)

features_samples_ratio = np.array(n_features_range) / n_train

plt.plot(
    features_samples_ratio,
    acc_clf1,
    linewidth=2,
    label="LDA",
    color="gold",
    linestyle="solid",
)
plt.plot(
    features_samples_ratio,
    acc_clf2,
    linewidth=2,
    label="LDA with Ledoit Wolf",
    color="navy",
    linestyle="dashed",
)
plt.plot(
    features_samples_ratio,
    acc_clf3,
    linewidth=2,
    label="LDA with OAS",
    color="red",
    linestyle="dotted",
)

plt.xlabel("n_features / n_samples")
plt.ylabel("Classification accuracy")

plt.legend(loc="lower left")
plt.ylim((0.65, 1.0))
plt.suptitle(
    "LDA (Linear Discriminant Analysis) vs. "
    + "\n"
    + "LDA with Ledoit Wolf vs. "
    + "\n"
    + "LDA with OAS (1 discriminative feature)"
)
plt.show()