Note
Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder
Comparing various online solvers#
An example showing how different online solvers perform on the hand-written digits dataset.
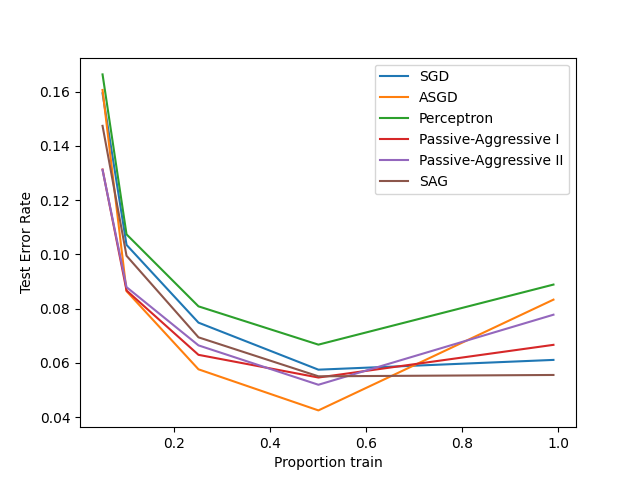
training SGD
training ASGD
training Perceptron
training Passive-Aggressive I
training Passive-Aggressive II
training SAG
# Author: Rob Zinkov <rob at zinkov dot com>
# License: BSD 3 clause
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.linear_model import (
LogisticRegression,
PassiveAggressiveClassifier,
Perceptron,
SGDClassifier,
)
from sklearn.model_selection import train_test_split
heldout = [0.95, 0.90, 0.75, 0.50, 0.01]
# Number of rounds to fit and evaluate an estimator.
rounds = 10
X, y = datasets.load_digits(return_X_y=True)
classifiers = [
("SGD", SGDClassifier(max_iter=110)),
("ASGD", SGDClassifier(max_iter=110, average=True)),
("Perceptron", Perceptron(max_iter=110)),
(
"Passive-Aggressive I",
PassiveAggressiveClassifier(max_iter=110, loss="hinge", C=1.0, tol=1e-4),
),
(
"Passive-Aggressive II",
PassiveAggressiveClassifier(
max_iter=110, loss="squared_hinge", C=1.0, tol=1e-4
),
),
(
"SAG",
LogisticRegression(max_iter=110, solver="sag", tol=1e-1, C=1.0e4 / X.shape[0]),
),
]
xx = 1.0 - np.array(heldout)
for name, clf in classifiers:
print("training %s" % name)
rng = np.random.RandomState(42)
yy = []
for i in heldout:
yy_ = []
for r in range(rounds):
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=i, random_state=rng
)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
yy_.append(1 - np.mean(y_pred == y_test))
yy.append(np.mean(yy_))
plt.plot(xx, yy, label=name)
plt.legend(loc="upper right")
plt.xlabel("Proportion train")
plt.ylabel("Test Error Rate")
plt.show()
Total running time of the script: (0 minutes 7.644 seconds)
Related examples
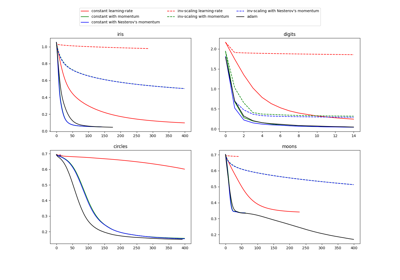
Compare Stochastic learning strategies for MLPClassifier
Compare Stochastic learning strategies for MLPClassifier