Note

Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder

Recursive feature elimination with cross-validation#

A Recursive Feature Elimination (RFE) example with automatic tuning of the number of features selected with cross-validation.

Data generation#

We build a classification task using 3 informative features. The introduction of 2 additional redundant (i.e. correlated) features has the effect that the selected features vary depending on the cross-validation fold. The remaining features are non-informative as they are drawn at random.

from sklearn.datasets import make_classification

X, y = make_classification(
    n_samples=500,
    n_features=15,
    n_informative=3,
    n_redundant=2,
    n_repeated=0,
    n_classes=8,
    n_clusters_per_class=1,
    class_sep=0.8,
    random_state=0,
)

Model training and selection#

We create the RFE object and compute the cross-validated scores. The scoring strategy “accuracy” optimizes the proportion of correctly classified samples.

from sklearn.feature_selection import RFECV
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import StratifiedKFold

min_features_to_select = 1  # Minimum number of features to consider
clf = LogisticRegression()
cv = StratifiedKFold(5)

rfecv = RFECV(
    estimator=clf,
    step=1,
    cv=cv,
    scoring="accuracy",
    min_features_to_select=min_features_to_select,
    n_jobs=2,
)
rfecv.fit(X, y)

print(f"Optimal number of features: {rfecv.n_features_}")

Optimal number of features: 3

In the present case, the model with 3 features (which corresponds to the true generative model) is found to be the most optimal.

Plot number of features VS. cross-validation scores#

import matplotlib.pyplot as plt

n_scores = len(rfecv.cv_results_["mean_test_score"])
plt.figure()
plt.xlabel("Number of features selected")
plt.ylabel("Mean test accuracy")
plt.errorbar(
    range(min_features_to_select, n_scores + min_features_to_select),
    rfecv.cv_results_["mean_test_score"],
    yerr=rfecv.cv_results_["std_test_score"],
)
plt.title("Recursive Feature Elimination \nwith correlated features")
plt.show()

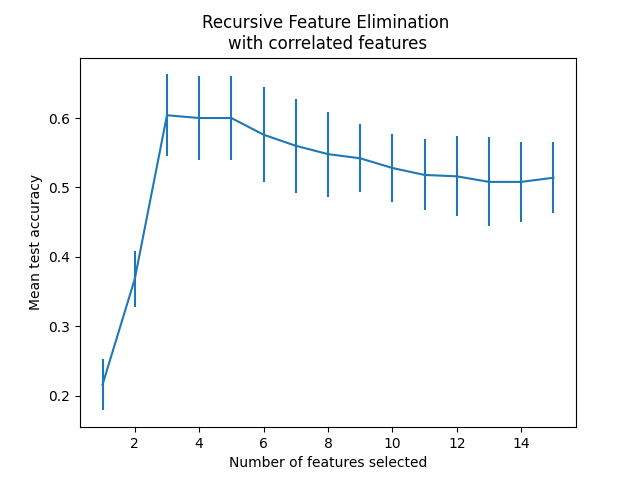
Recursive Feature Elimination with correlated features

From the plot above one can further notice a plateau of equivalent scores (similar mean value and overlapping errorbars) for 3 to 5 selected features. This is the result of introducing correlated features. Indeed, the optimal model selected by the RFE can lie within this range, depending on the cross-validation technique. The test accuracy decreases above 5 selected features, this is, keeping non-informative features leads to over-fitting and is therefore detrimental for the statistical performance of the models.

Total running time of the script: (0 minutes 0.417 seconds)