Note

Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder

Successive Halving Iterations#

This example illustrates how a successive halving search (HalvingGridSearchCV and HalvingRandomSearchCV) iteratively chooses the best parameter combination out of multiple candidates.

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from scipy.stats import randint

from sklearn import datasets
from sklearn.ensemble import RandomForestClassifier
from sklearn.experimental import enable_halving_search_cv  # noqa
from sklearn.model_selection import HalvingRandomSearchCV

We first define the parameter space and train a HalvingRandomSearchCV instance.

rng = np.random.RandomState(0)

X, y = datasets.make_classification(n_samples=400, n_features=12, random_state=rng)

clf = RandomForestClassifier(n_estimators=20, random_state=rng)

param_dist = {
    "max_depth": [3, None],
    "max_features": randint(1, 6),
    "min_samples_split": randint(2, 11),
    "bootstrap": [True, False],
    "criterion": ["gini", "entropy"],
}

rsh = HalvingRandomSearchCV(
    estimator=clf, param_distributions=param_dist, factor=2, random_state=rng
)
rsh.fit(X, y)

HalvingRandomSearchCV(estimator=RandomForestClassifier(n_estimators=20,
                                                       random_state=RandomState(MT19937) at 0x7F76A0C36440),
                      factor=2,
                      param_distributions={'bootstrap': [True, False],
                                           'criterion': ['gini', 'entropy'],
                                           'max_depth': [3, None],
                                           'max_features': <scipy.stats._distn_infrastructure.rv_discrete_frozen object at 0x7f76a0d3ca00>,
                                           'min_samples_split': <scipy.stats._distn_infrastructure.rv_discrete_frozen object at 0x7f76cc708310>},
                      random_state=RandomState(MT19937) at 0x7F76A0C36440)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

We can now use the cv_results_ attribute of the search estimator to inspect and plot the evolution of the search.

results = pd.DataFrame(rsh.cv_results_)
results["params_str"] = results.params.apply(str)
results.drop_duplicates(subset=("params_str", "iter"), inplace=True)
mean_scores = results.pivot(
    index="iter", columns="params_str", values="mean_test_score"
)
ax = mean_scores.plot(legend=False, alpha=0.6)

labels = [
    f"iter={i}\nn_samples={rsh.n_resources_[i]}\nn_candidates={rsh.n_candidates_[i]}"
    for i in range(rsh.n_iterations_)
]

ax.set_xticks(range(rsh.n_iterations_))
ax.set_xticklabels(labels, rotation=45, multialignment="left")
ax.set_title("Scores of candidates over iterations")
ax.set_ylabel("mean test score", fontsize=15)
ax.set_xlabel("iterations", fontsize=15)
plt.tight_layout()
plt.show()

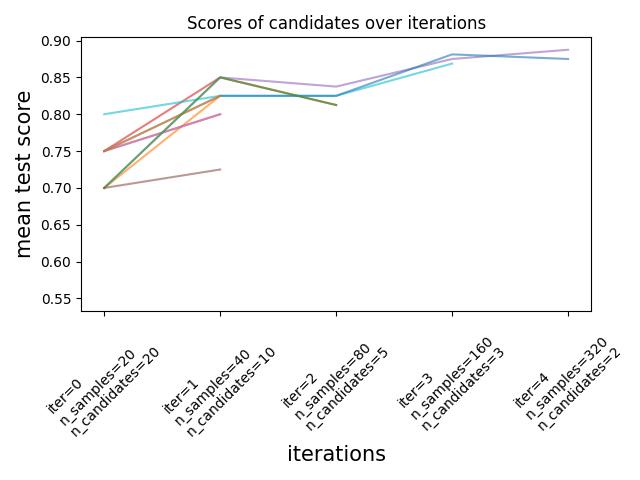
Number of candidates and amount of resource at each iteration#

At the first iteration, a small amount of resources is used. The resource here is the number of samples that the estimators are trained on. All candidates are evaluated.

At the second iteration, only the best half of the candidates is evaluated. The number of allocated resources is doubled: candidates are evaluated on twice as many samples.

This process is repeated until the last iteration, where only 2 candidates are left. The best candidate is the candidate that has the best score at the last iteration.

Total running time of the script: (0 minutes 4.327 seconds)