sklearn.cluster.OPTICS

class sklearn.cluster.OPTICS(*, min_samples=5, max_eps=inf, metric='minkowski', p=2, metric_params=None, cluster_method='xi', eps=None, xi=0.05, predecessor_correction=True, min_cluster_size=None, algorithm='auto', leaf_size=30, memory=None, n_jobs=None)

Estimate clustering structure from vector array.

OPTICS (Ordering Points To Identify the Clustering Structure), closely related to DBSCAN, finds core sample of high density and expands clusters from them [1]. Unlike DBSCAN, keeps cluster hierarchy for a variable neighborhood radius. Better suited for usage on large datasets than the current sklearn implementation of DBSCAN.

Clusters are then extracted using a DBSCAN-like method (cluster_method = ‘dbscan’) or an automatic technique proposed in [1] (cluster_method = ‘xi’).

This implementation deviates from the original OPTICS by first performing k-nearest-neighborhood searches on all points to identify core sizes, then computing only the distances to unprocessed points when constructing the cluster order. Note that we do not employ a heap to manage the expansion candidates, so the time complexity will be O(n^2).

Read more in the User Guide.

Parameters:

min_samplesint > 1 or float between 0 and 1, default=5

The number of samples in a neighborhood for a point to be considered as a core point. Also, up and down steep regions can’t have more than min_samples consecutive non-steep points. Expressed as an absolute number or a fraction of the number of samples (rounded to be at least 2).

max_epsfloat, default=np.inf

The maximum distance between two samples for one to be considered as in the neighborhood of the other. Default value of np.inf will identify clusters across all scales; reducing max_eps will result in shorter run times.

metricstr or callable, default=’minkowski’

Metric to use for distance computation. Any metric from scikit-learn or scipy.spatial.distance can be used.

If metric is a callable function, it is called on each pair of instances (rows) and the resulting value recorded. The callable should take two arrays as input and return one value indicating the distance between them. This works for Scipy’s metrics, but is less efficient than passing the metric name as a string. If metric is “precomputed”, X is assumed to be a distance matrix and must be square.

Valid values for metric are:

• from scikit-learn: [‘cityblock’, ‘cosine’, ‘euclidean’, ‘l1’, ‘l2’, ‘manhattan’]

• from scipy.spatial.distance: [‘braycurtis’, ‘canberra’, ‘chebyshev’, ‘correlation’, ‘dice’, ‘hamming’, ‘jaccard’, ‘kulsinski’, ‘mahalanobis’, ‘minkowski’, ‘rogerstanimoto’, ‘russellrao’, ‘seuclidean’, ‘sokalmichener’, ‘sokalsneath’, ‘sqeuclidean’, ‘yule’]

Sparse matrices are only supported by scikit-learn metrics. See the documentation for scipy.spatial.distance for details on these metrics.

Note

'kulsinski' is deprecated from SciPy 1.9 and will removed in SciPy 1.11.

pfloat, default=2

Parameter for the Minkowski metric from pairwise_distances. When p = 1, this is equivalent to using manhattan_distance (l1), and euclidean_distance (l2) for p = 2. For arbitrary p, minkowski_distance (l_p) is used.

metric_paramsdict, default=None

Additional keyword arguments for the metric function.

cluster_methodstr, default=’xi’

The extraction method used to extract clusters using the calculated reachability and ordering. Possible values are “xi” and “dbscan”.

epsfloat, default=None

The maximum distance between two samples for one to be considered as in the neighborhood of the other. By default it assumes the same value as max_eps. Used only when cluster_method='dbscan'.

xifloat between 0 and 1, default=0.05

Determines the minimum steepness on the reachability plot that constitutes a cluster boundary. For example, an upwards point in the reachability plot is defined by the ratio from one point to its successor being at most 1-xi. Used only when cluster_method='xi'.

predecessor_correctionbool, default=True

Correct clusters according to the predecessors calculated by OPTICS [2]. This parameter has minimal effect on most datasets. Used only when cluster_method='xi'.

min_cluster_sizeint > 1 or float between 0 and 1, default=None

Minimum number of samples in an OPTICS cluster, expressed as an absolute number or a fraction of the number of samples (rounded to be at least 2). If None, the value of min_samples is used instead. Used only when cluster_method='xi'.

algorithm{‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}, default=’auto’

Algorithm used to compute the nearest neighbors:

• ‘ball_tree’ will use BallTree.

• ‘kd_tree’ will use KDTree.

• ‘brute’ will use a brute-force search.

• ‘auto’ (default) will attempt to decide the most appropriate algorithm based on the values passed to fit method.

Note: fitting on sparse input will override the setting of this parameter, using brute force.

leaf_sizeint, default=30

Leaf size passed to BallTree or KDTree. This can affect the speed of the construction and query, as well as the memory required to store the tree. The optimal value depends on the nature of the problem.

memorystr or object with the joblib.Memory interface, default=None

Used to cache the output of the computation of the tree. By default, no caching is done. If a string is given, it is the path to the caching directory.

n_jobsint, default=None

The number of parallel jobs to run for neighbors search. None means 1 unless in a joblib.parallel_backend context. -1 means using all processors. See Glossary for more details.

Attributes:

labels_ndarray of shape (n_samples,)

Cluster labels for each point in the dataset given to fit(). Noisy samples and points which are not included in a leaf cluster of cluster_hierarchy_ are labeled as -1.

reachability_ndarray of shape (n_samples,)

Reachability distances per sample, indexed by object order. Use clust.reachability_[clust.ordering_] to access in cluster order.

ordering_ndarray of shape (n_samples,)

The cluster ordered list of sample indices.

core_distances_ndarray of shape (n_samples,)

Distance at which each sample becomes a core point, indexed by object order. Points which will never be core have a distance of inf. Use clust.core_distances_[clust.ordering_] to access in cluster order.

predecessor_ndarray of shape (n_samples,)

Point that a sample was reached from, indexed by object order. Seed points have a predecessor of -1.

cluster_hierarchy_ndarray of shape (n_clusters, 2)

The list of clusters in the form of [start, end] in each row, with all indices inclusive. The clusters are ordered according to (end, -start) (ascending) so that larger clusters encompassing smaller clusters come after those smaller ones. Since labels_ does not reflect the hierarchy, usually len(cluster_hierarchy_) > np.unique(optics.labels_). Please also note that these indices are of the ordering_, i.e. X[ordering_][start:end + 1] form a cluster. Only available when cluster_method='xi'.

n_features_in_int

Number of features seen during fit.

New in version 0.24.

feature_names_in_ndarray of shape (n_features_in_,)

Names of features seen during fit. Defined only when X has feature names that are all strings.

New in version 1.0.

See also

DBSCAN

A similar clustering for a specified neighborhood radius (eps). Our implementation is optimized for runtime.

References

[1] (1,2)

Ankerst, Mihael, Markus M. Breunig, Hans-Peter Kriegel, and Jörg Sander. “OPTICS: ordering points to identify the clustering structure.” ACM SIGMOD Record 28, no. 2 (1999): 49-60.

[2]

Schubert, Erich, Michael Gertz. “Improving the Cluster Structure Extracted from OPTICS Plots.” Proc. of the Conference “Lernen, Wissen, Daten, Analysen” (LWDA) (2018): 318-329.

Examples

>>> from sklearn.cluster import OPTICS
>>> import numpy as np
>>> X = np.array([[1, 2], [2, 5], [3, 6],
...               [8, 7], [8, 8], [7, 3]])
>>> clustering = OPTICS(min_samples=2).fit(X)
>>> clustering.labels_
array([0, 0, 0, 1, 1, 1])

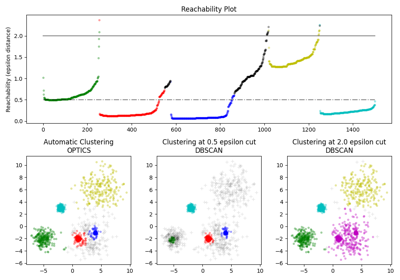
For a more detailed example see Demo of OPTICS clustering algorithm.

Methods

fit(X[, y])	Perform OPTICS clustering.
fit_predict(X[, y])	Perform clustering on X and returns cluster labels.
get_metadata_routing()	Get metadata routing of this object.
get_params([deep])	Get parameters for this estimator.
set_params(**params)	Set the parameters of this estimator.

fit(X, y=None)

Perform OPTICS clustering.

Extracts an ordered list of points and reachability distances, and performs initial clustering using max_eps distance specified at OPTICS object instantiation.

Parameters:

X{ndarray, sparse matrix} of shape (n_samples, n_features), or (n_samples, n_samples) if metric=’precomputed’

A feature array, or array of distances between samples if metric=’precomputed’. If a sparse matrix is provided, it will be converted into CSR format.

yIgnored

Not used, present for API consistency by convention.

Returns:

selfobject

Returns a fitted instance of self.

fit_predict(X, y=None, **kwargs)

Perform clustering on X and returns cluster labels.

Parameters:

Xarray-like of shape (n_samples, n_features)

Input data.

yIgnored

Not used, present for API consistency by convention.

**kwargsdict

Arguments to be passed to fit.

New in version 1.4.

Returns:

labelsndarray of shape (n_samples,), dtype=np.int64

Cluster labels.

get_metadata_routing()

Get metadata routing of this object.

Please check User Guide on how the routing mechanism works.

Returns:

routingMetadataRequest

A MetadataRequest encapsulating routing information.

get_params(deep=True)

Get parameters for this estimator.

Parameters:

deepbool, default=True

If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

paramsdict

Parameter names mapped to their values.

set_params(**params)

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters:

**paramsdict

Estimator parameters.

Returns:

selfestimator instance

Estimator instance.

Examples using sklearn.cluster.OPTICS

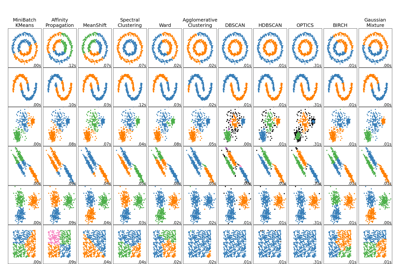
Comparing different clustering algorithms on toy datasets

Comparing different clustering algorithms on toy datasets

Demo of OPTICS clustering algorithm

Demo of OPTICS clustering algorithm